La chimie du carbone et des carbonates dans l'océan contrôle le taux de CO2 atmosphérique ainsi que la précipitation de carbonates
Le carbone inorganique dissout existe sous 3 formes: ![\left[CO_{2d}\right]](eq_tex_1-ss-partie-var-athmo/equation2.png) ,
, ![\left[HCO_3^-\right]](eq_tex_1-ss-partie-var-athmo/equation3.png) ,
, ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation4.png) .
On a les constantes d'équilibres chimiques suivantes:
.
On a les constantes d'équilibres chimiques suivantes:
![K_0 = \frac {\left[ CO_{2d} \right]} {pCO_2}](eq_tex_1-ss-partie-var-athmo/equation5.png)
dissolution du gaz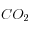
![K_1 = \frac{\left[H^+\right]\left[HCO_3^-\right]}{\left[CO_{2d}\right]}](eq_tex_1-ss-partie-var-athmo/equation7.png)
1ere dissociation
![K_2 = \frac{\left[H^+\right]\left[CO_3^=\right]}{\left[HCO_3^-\right]}](eq_tex_1-ss-partie-var-athmo/equation8.png)
2eme dissociation
![K_S = \left[Ca^{2+}\right]\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation9.png)
dissolution du carbonate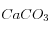 qui dépendent de la température, la salinité, la pression, etc… mais que l'on supposera ici vraiment constantes.
qui dépendent de la température, la salinité, la pression, etc… mais que l'on supposera ici vraiment constantes.
On introduit les quantités conservatrices suivantes:
Le carbone total (en anglais DIC: dissolved inorganic carbon):
![C=\left[CO_{2d}\right]+\left[HCO_3^-\right]}+\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation11.png)
L'alcalinité (liée à l'équilibre des charges):
![A=2\left[CO_3^=\right]+\left[HCO_3^-\right]+borates+termes\ petits](eq_tex_1-ss-partie-var-athmo/equation12.png)
Lorsqu'on ajoute 1 mole de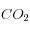 : ∆C = +1, ∆A = 0
: ∆C = +1, ∆A = 0
Lorsqu'on dissout 1 mole de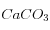 : ∆C = +1, ∆A = +2
: ∆C = +1, ∆A = +2
Si on néglige![\left[CO_{2d} \right]](eq_tex_1-ss-partie-var-athmo/equation15.png) (~ 1%) devant les autres termes (
(~ 1%) devant les autres termes (![\left[ HCO_3^-\right]](eq_tex_1-ss-partie-var-athmo/equation16.png) ~ 90% et
~ 90% et ![\left[ CO_3^= \right]](eq_tex_1-ss-partie-var-athmo/equation17.png) ~ 10%), on obtient:
~ 10%), on obtient:
![C\approx \left[ CO_3^= \right]+\left[ HCO_3^- \right]](eq_tex_1-ss-partie-var-athmo/equation18.png)
![A \approx 2\left[ CO_3^= \right]+\left[ HCO_3^- \right]](eq_tex_1-ss-partie-var-athmo/equation19.png)
d'où :
![\left[ CO_3^= \right]\approx A - C](eq_tex_1-ss-partie-var-athmo/equation20.png)
![\left[ HCO_3^- \right] \approx 2\ C - A](eq_tex_1-ss-partie-var-athmo/equation21.png)
On calcule les variations :
![\Delta\left[ CO_3^= \right] \approx \Delta A - \Delta C](eq_tex_1-ss-partie-var-athmo/equation22.png)
![\Delta\left[ HCO_3^- \right] \approx 2 \Delta C - \Delta A](eq_tex_1-ss-partie-var-athmo/equation23.png)
![\left[H^+\right] = \frac{K_2 \left[HCO_3^-\right]}{\left[CO_3^=\right]}](eq_tex_1-ss-partie-var-athmo/equation24.png) ;
;
![pH = pK_2 - \log_{10}\left(\frac{\left[HCO_3^-\right]}{\left[CO_3^=\right]}\right)](eq_tex_1-ss-partie-var-athmo/equation25.png)
![\left[CO_{2d}\right] = \frac{\left[H^+\right]\left[HCO_3^-\right]} {K_1} =\frac{(\frac{K_2}{K_1}) \left[HCO_3^-\right]^2}{\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation26.png)
d'où:
![\Delta pH \approx - \left(\frac{\Delta\left[HCO_3^-\right]}{\left[HCO_3^-\right]\right) + \left(\frac{\Delta\left[CO_3^=\right]}{\left[CO_3^=\right]\right)](eq_tex_1-ss-partie-var-athmo/equation27.png)
![\frac {\Delta pCO_2}{pCO_2} \approx 2 \left(\frac{\Delta\left[HCO_3^-\right]}{\left[HCO_3^-\right]\right) - \left(\frac{\Delta\left[CO_3^=\right]}{\left[CO_3^=\right]\right)](eq_tex_1-ss-partie-var-athmo/equation28.png)
![\left[CO_{2d}\right]](eq_tex_1-ss-partie-var-athmo/equation2.png) ,
, ![\left[HCO_3^-\right]](eq_tex_1-ss-partie-var-athmo/equation3.png) ,
, ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation4.png) .
On a les constantes d'équilibres chimiques suivantes:
.
On a les constantes d'équilibres chimiques suivantes:![K_0 = \frac {\left[ CO_{2d} \right]} {pCO_2}](eq_tex_1-ss-partie-var-athmo/equation5.png)
dissolution du gaz
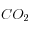
![K_1 = \frac{\left[H^+\right]\left[HCO_3^-\right]}{\left[CO_{2d}\right]}](eq_tex_1-ss-partie-var-athmo/equation7.png)
1ere dissociation
![K_2 = \frac{\left[H^+\right]\left[CO_3^=\right]}{\left[HCO_3^-\right]}](eq_tex_1-ss-partie-var-athmo/equation8.png)
2eme dissociation
![K_S = \left[Ca^{2+}\right]\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation9.png)
dissolution du carbonate
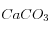 qui dépendent de la température, la salinité, la pression, etc… mais que l'on supposera ici vraiment constantes.
qui dépendent de la température, la salinité, la pression, etc… mais que l'on supposera ici vraiment constantes.On introduit les quantités conservatrices suivantes:
Le carbone total (en anglais DIC: dissolved inorganic carbon):
![C=\left[CO_{2d}\right]+\left[HCO_3^-\right]}+\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation11.png)
L'alcalinité (liée à l'équilibre des charges):
![A=2\left[CO_3^=\right]+\left[HCO_3^-\right]+borates+termes\ petits](eq_tex_1-ss-partie-var-athmo/equation12.png)
Lorsqu'on ajoute 1 mole de
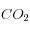 : ∆C = +1, ∆A = 0
: ∆C = +1, ∆A = 0Lorsqu'on dissout 1 mole de
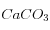 : ∆C = +1, ∆A = +2
: ∆C = +1, ∆A = +2Si on néglige
![\left[CO_{2d} \right]](eq_tex_1-ss-partie-var-athmo/equation15.png) (~ 1%) devant les autres termes (
(~ 1%) devant les autres termes (![\left[ HCO_3^-\right]](eq_tex_1-ss-partie-var-athmo/equation16.png) ~ 90% et
~ 90% et ![\left[ CO_3^= \right]](eq_tex_1-ss-partie-var-athmo/equation17.png) ~ 10%), on obtient:
~ 10%), on obtient:![C\approx \left[ CO_3^= \right]+\left[ HCO_3^- \right]](eq_tex_1-ss-partie-var-athmo/equation18.png)
![A \approx 2\left[ CO_3^= \right]+\left[ HCO_3^- \right]](eq_tex_1-ss-partie-var-athmo/equation19.png)
d'où :
![\left[ CO_3^= \right]\approx A - C](eq_tex_1-ss-partie-var-athmo/equation20.png)
![\left[ HCO_3^- \right] \approx 2\ C - A](eq_tex_1-ss-partie-var-athmo/equation21.png)
On calcule les variations :
![\Delta\left[ CO_3^= \right] \approx \Delta A - \Delta C](eq_tex_1-ss-partie-var-athmo/equation22.png)
![\Delta\left[ HCO_3^- \right] \approx 2 \Delta C - \Delta A](eq_tex_1-ss-partie-var-athmo/equation23.png)
![\left[H^+\right] = \frac{K_2 \left[HCO_3^-\right]}{\left[CO_3^=\right]}](eq_tex_1-ss-partie-var-athmo/equation24.png) ;
;![pH = pK_2 - \log_{10}\left(\frac{\left[HCO_3^-\right]}{\left[CO_3^=\right]}\right)](eq_tex_1-ss-partie-var-athmo/equation25.png)
![\left[CO_{2d}\right] = \frac{\left[H^+\right]\left[HCO_3^-\right]} {K_1} =\frac{(\frac{K_2}{K_1}) \left[HCO_3^-\right]^2}{\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation26.png)
d'où:
![\Delta pH \approx - \left(\frac{\Delta\left[HCO_3^-\right]}{\left[HCO_3^-\right]\right) + \left(\frac{\Delta\left[CO_3^=\right]}{\left[CO_3^=\right]\right)](eq_tex_1-ss-partie-var-athmo/equation27.png)
![\frac {\Delta pCO_2}{pCO_2} \approx 2 \left(\frac{\Delta\left[HCO_3^-\right]}{\left[HCO_3^-\right]\right) - \left(\frac{\Delta\left[CO_3^=\right]}{\left[CO_3^=\right]\right)](eq_tex_1-ss-partie-var-athmo/equation28.png)
Figure 1
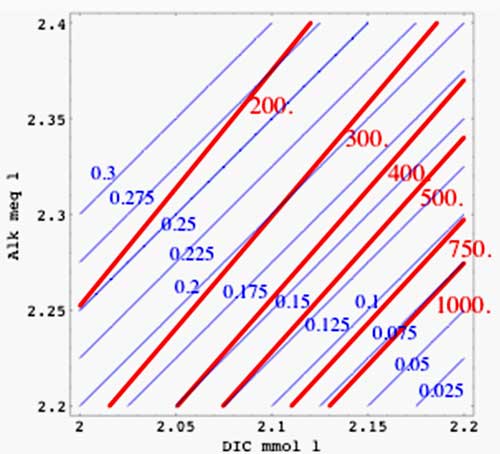
Légende
isolignes pour 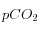 (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation30.png) (en mmol/l, en bleu) en fonction du carbone inorganique total C (DIC en anglais) et de l'alcalinité A, en utilisant l'approximation drastique utilisée ici (avec les constantes d'équilibre prises à T=288K et S=35‰). A comparer aux 2 figures ci-dessous…
(en mmol/l, en bleu) en fonction du carbone inorganique total C (DIC en anglais) et de l'alcalinité A, en utilisant l'approximation drastique utilisée ici (avec les constantes d'équilibre prises à T=288K et S=35‰). A comparer aux 2 figures ci-dessous…
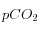 (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation30.png) (en mmol/l, en bleu) en fonction du carbone inorganique total C (DIC en anglais) et de l'alcalinité A, en utilisant l'approximation drastique utilisée ici (avec les constantes d'équilibre prises à T=288K et S=35‰). A comparer aux 2 figures ci-dessous…
(en mmol/l, en bleu) en fonction du carbone inorganique total C (DIC en anglais) et de l'alcalinité A, en utilisant l'approximation drastique utilisée ici (avec les constantes d'équilibre prises à T=288K et S=35‰). A comparer aux 2 figures ci-dessous…
Figure 2
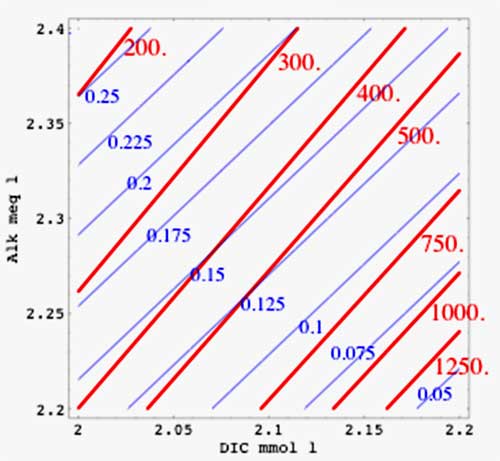
Légende
isolignes pour  (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation32.png) (en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=288K et S=35‰
(en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=288K et S=35‰
 (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation32.png) (en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=288K et S=35‰
(en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=288K et S=35‰
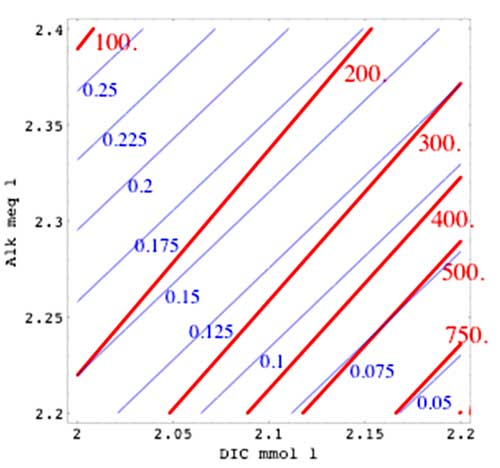
Figure 3
Légende
isolignes pour  (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation34.png) (en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=275K et S=33‰
(en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=275K et S=33‰
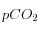 (en ppm, en rouge) et pour
(en ppm, en rouge) et pour ![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation34.png) (en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=275K et S=33‰
(en mmol/l, en bleu) avec un calcul plus réaliste (en tenant compte des borates) pour T=275K et S=33‰
Comme on peut le voir sur les figures ci-dessus, l'approximation que l'on a fait n'est pas très bonne numériquement, mais l'allure des courbes (en particulier leur pente) est raisonnablement reproduite. Par ailleurs, la température a un effet très important sur les constantes d'équilibre, en particulier sur la solubilité du 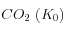 .
.
Si l'on part d'un océan "actuel" (en exprimant tout en GtC au lieu de moles) avec C = 38 000 GtC et A = 42 000 GtC (soit
![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation37.png) = 4000 GtC et
= 4000 GtC et ![\left[HCO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation38.png) = 34000 GtC). Une injection de 1000 GtC de
= 34000 GtC). Une injection de 1000 GtC de 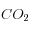 produit la perturbation (après équilibre océan-atmosphère, soit quelques siècles ou plus):
produit la perturbation (après équilibre océan-atmosphère, soit quelques siècles ou plus):
 ,
, 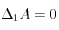
soit:![\Delta_1\left[CO_3^=\right] \approx - 1000 \ GTC](eq_tex_1-ss-partie-var-athmo/equation42.png) ;
; ![\Delta_1\left[HCO_3^-\right] \approx - 2000 \ GTC](eq_tex_1-ss-partie-var-athmo/equation43.png)
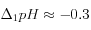 ;
; 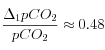 (= augmentation de 48 %)
(= augmentation de 48 %)
La diminution de![\left[HCO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation46.png) va entrainer une dissolution de
va entrainer une dissolution de 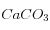 , jusqu'à rétablir le produit de solubilité
, jusqu'à rétablir le produit de solubilité ![K_S = \left[Ca^{2+}\right]\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation48.png) (après équilibre océan-carbonate, soit quelques millénaires ou plus): comme la concentration en
(après équilibre océan-carbonate, soit quelques millénaires ou plus): comme la concentration en 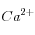 change peu, on va en fait rétablir la concentration initiale en
change peu, on va en fait rétablir la concentration initiale en 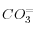 . C'est la compensation des carbonates. Pour la dissolution d'une mole de
. C'est la compensation des carbonates. Pour la dissolution d'une mole de 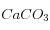 ,
, 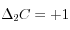 ,
, 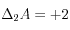 . Donc pour obtenir
. Donc pour obtenir ![(\Delta_1 + \Delta_2)\left[CO_3^=\right] = (\Delta_1 + \Delta_2)(A - C) =0](eq_tex_1-ss-partie-var-athmo/equation54.png) , il faut dissoudre 1000 GtC de
, il faut dissoudre 1000 GtC de 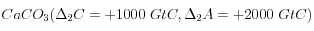 .
.
Au total:
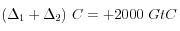 ;
; 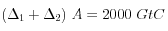
![(\Delta_1 + \Delta_2)\left[CO_3^=\right] \approx 0](eq_tex_1-ss-partie-var-athmo/equation58.png) ;
;![(\Delta_1 + \Delta_2)\left[HCO_3^-\right] \approx + 2000 \ GtC](eq_tex_1-ss-partie-var-athmo/equation59.png)
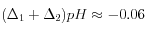 ;
; 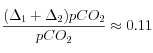 (= augmentation de 11 %)
(= augmentation de 11 %)
Pour revenir aux conditions initiales (après quelques centaines de milliers d'années), il faut invoquer la dissolution des silicates. En effet, comme cela est détaillé plus bas, celle-ci permet d'utiliser 1 pour produire 1 ion
pour produire 1 ion 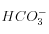 dissout dans l'eau, soit le bilan
dissout dans l'eau, soit le bilan 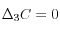 ,
, 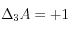 .
Si l'on impose l'équilibre des carbonates
.
Si l'on impose l'équilibre des carbonates 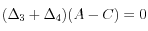 , il faut en plus précipiter du carbonate
, il faut en plus précipiter du carbonate 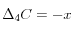 ,
,  :
:
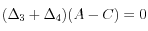 =>
=>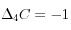 ,
, 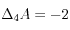
On précipite donc 1 mole de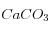 pour chaque mole de
pour chaque mole de 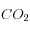 utilisée par la dissolution des silicates. Pour
utilisée par la dissolution des silicates. Pour 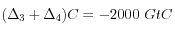 et
et 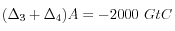 , on revient bien aux conditions initiales, c'est-à-dire
, on revient bien aux conditions initiales, c'est-à-dire 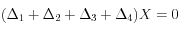 .
.
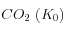 .
.Si l'on part d'un océan "actuel" (en exprimant tout en GtC au lieu de moles) avec C = 38 000 GtC et A = 42 000 GtC (soit

![\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation37.png) = 4000 GtC et
= 4000 GtC et ![\left[HCO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation38.png) = 34000 GtC). Une injection de 1000 GtC de
= 34000 GtC). Une injection de 1000 GtC de 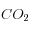 produit la perturbation (après équilibre océan-atmosphère, soit quelques siècles ou plus):
produit la perturbation (après équilibre océan-atmosphère, soit quelques siècles ou plus): ,
, 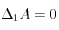
soit:
![\Delta_1\left[CO_3^=\right] \approx - 1000 \ GTC](eq_tex_1-ss-partie-var-athmo/equation42.png) ;
; ![\Delta_1\left[HCO_3^-\right] \approx - 2000 \ GTC](eq_tex_1-ss-partie-var-athmo/equation43.png)
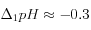 ;
; 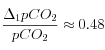 (= augmentation de 48 %)
(= augmentation de 48 %)La diminution de
![\left[HCO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation46.png) va entrainer une dissolution de
va entrainer une dissolution de 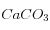 , jusqu'à rétablir le produit de solubilité
, jusqu'à rétablir le produit de solubilité ![K_S = \left[Ca^{2+}\right]\left[CO_3^=\right]](eq_tex_1-ss-partie-var-athmo/equation48.png) (après équilibre océan-carbonate, soit quelques millénaires ou plus): comme la concentration en
(après équilibre océan-carbonate, soit quelques millénaires ou plus): comme la concentration en 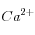 change peu, on va en fait rétablir la concentration initiale en
change peu, on va en fait rétablir la concentration initiale en 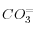 . C'est la compensation des carbonates. Pour la dissolution d'une mole de
. C'est la compensation des carbonates. Pour la dissolution d'une mole de 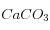 ,
, 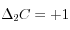 ,
, 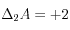 . Donc pour obtenir
. Donc pour obtenir ![(\Delta_1 + \Delta_2)\left[CO_3^=\right] = (\Delta_1 + \Delta_2)(A - C) =0](eq_tex_1-ss-partie-var-athmo/equation54.png) , il faut dissoudre 1000 GtC de
, il faut dissoudre 1000 GtC de 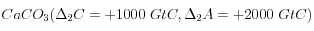 .
.Au total:
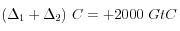 ;
; 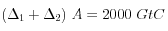
![(\Delta_1 + \Delta_2)\left[CO_3^=\right] \approx 0](eq_tex_1-ss-partie-var-athmo/equation58.png) ;
;![(\Delta_1 + \Delta_2)\left[HCO_3^-\right] \approx + 2000 \ GtC](eq_tex_1-ss-partie-var-athmo/equation59.png)
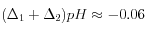 ;
; 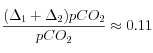 (= augmentation de 11 %)
(= augmentation de 11 %)Pour revenir aux conditions initiales (après quelques centaines de milliers d'années), il faut invoquer la dissolution des silicates. En effet, comme cela est détaillé plus bas, celle-ci permet d'utiliser 1
 pour produire 1 ion
pour produire 1 ion 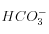 dissout dans l'eau, soit le bilan
dissout dans l'eau, soit le bilan 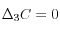 ,
, 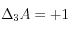 .
Si l'on impose l'équilibre des carbonates
.
Si l'on impose l'équilibre des carbonates 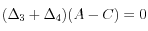 , il faut en plus précipiter du carbonate
, il faut en plus précipiter du carbonate 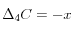 ,
,  :
: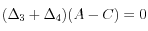 =>
=>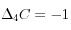 ,
, 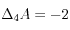
On précipite donc 1 mole de
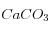 pour chaque mole de
pour chaque mole de 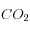 utilisée par la dissolution des silicates. Pour
utilisée par la dissolution des silicates. Pour 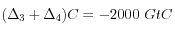 et
et 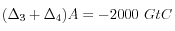 , on revient bien aux conditions initiales, c'est-à-dire
, on revient bien aux conditions initiales, c'est-à-dire 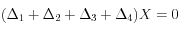 .
.
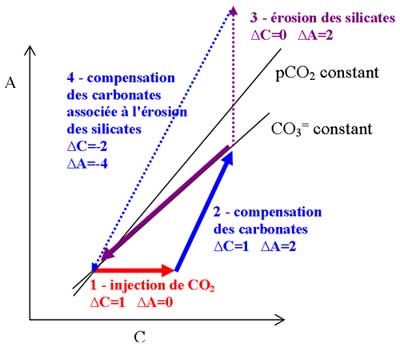
Schéma
Légende
Schéma reprenant les différentes étapes associées à une injection de 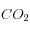 dans l'océan. L'érosion des silicates (étape 3) étant très lente par rapport à la compensation des carbonates (étape 4), le chemin de "retour" est la flèche pleine violette à concentration en carbonate constante.
dans l'océan. L'érosion des silicates (étape 3) étant très lente par rapport à la compensation des carbonates (étape 4), le chemin de "retour" est la flèche pleine violette à concentration en carbonate constante.
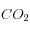 dans l'océan. L'érosion des silicates (étape 3) étant très lente par rapport à la compensation des carbonates (étape 4), le chemin de "retour" est la flèche pleine violette à concentration en carbonate constante.
dans l'océan. L'érosion des silicates (étape 3) étant très lente par rapport à la compensation des carbonates (étape 4), le chemin de "retour" est la flèche pleine violette à concentration en carbonate constante.